搞改革你反射
漫反射
搞改革你反射
漫反射
shader 实时编译。
多用float Half
写法要符合规范。
建议使用SV_Position.
不知道再讲什么。
rgb 红绿蓝。
有点不知道在干啥。
Shader "Unlit/003"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_Color("Color" , Color) = (1,1,1,1)
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
//#include "UnityCG.cginc"
//只有在CGPROGRAM内再次定义一个与属性块内名字与类型相同的变量,属性块对应的变量才能起作用
fixed4 _Color;
struct a2v//a application dao vert
{
//用模型顶点填充v变量
float4 vertex:POSITION;
//用模型的法线填充n变量
float3 normal:NORMAL;
//用模型的第一套uv填充texcoord
float4 texcoord: TEXCOORD0;
};
struct v2f// v vert dao frag
{
//SV_POSITION语义告诉unity : pos为裁剪空间中的位置信息
float4 pos:SV_POSITION;
//COLOR0 语义可以储存颜色信息
fixed3 color:COLOR0;
};
v2f vert(a2v v)
{
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
//将 【-1,1】转变为【0,1】 x/2 + 0.5;
o.color = v.normal * 0.5 +fixed3(0.5,0.5,0.5);
return o;
}
fixed4 frag(v2f i):SV_TARGET
{
fixed3 c = i.color;
//.xyzw .rgba .x .y .xw
c*=_Color.rgb;
//return fixed4(0,0,0,1);
return fixed4(c, 1);
}
ENDCG
}
}
}
vertex 顶点
fragment 片元
// 定义Shader路径和名称(在材质面板中的显示层级)
Shader "Unlit/002"
{
// 材质属性声明块(会在Inspector面板显示)
Properties
{
// 声明2D纹理属性,默认白色纹理(实际未使用)
_MainTex ("Texture", 2D) = "white" {}
}
// 子着色器块(核心逻辑)
SubShader
{
// 渲染标签设置(影响渲染管线行为)
Tags {
"RenderType"="Opaque" // 标识为不透明物体,用于后处理筛选
}
LOD 100 // 细节层级,当设备性能不足时选择更简化的SubShader
// 渲染通道(包含实际渲染逻辑)
Pass
{
// 开始CG编程(HLSL语法)
CGPROGRAM
// 声明顶点着色器函数名为 vert
#pragma vertex vert
// 声明片元着色器函数名为 frag
#pragma fragment frag
////// 顶点着色器输入输出定义 //////
// 输入参数:顶点位置(POSITION语义)
// 输出参数:裁剪空间坐标(SV_POSITION语义)
float4 vert(float4 v : POSITION) : SV_POSITION
{
// 模型空间 → 裁剪空间坐标转换(核心变换)
return UnityObjectToClipPos(v);
}
////// 片元着色器输出定义 //////
// 输出参数:目标颜色(SV_TARGET语义)
fixed4 frag() : SV_TARGET
{
// 返回纯白色(RGBA通道均为1)
return fixed4(1,1,1,1);
}
ENDCG // 结束CG代码块
}
}
}
三维变二维。
仿射变换通过线性与平移操作的结合,成为几何变换的通用工具
图像变换。
平移操作,保持几何不变性。
用于物体旋转与反射。
齐次空间 最后一个w
统一性
其次空间,无限远的点最终会相交。
A 的转置才为伴随矩阵 转置矩阵就是行变列,列变行
矩阵相乘 就是行*后边的一列 作为一个元素。
逆矩阵 *矩阵等于单位矩阵。
线性变换的可逆性,就是能放进去,也能放回来。用于还原。

伴随矩阵
每个元素都是矩阵里每个元素的代数余子式 叫伴随矩阵。加转置。
代数余子式,根据下标 结果有正负号。 奇数为负 偶数为正。
高维行列式转低维 通过按行按列展开。
行列式的结果等于一行的单个数乘以他们的 代数余子式 下标为奇数,前边符号为减 下表为偶数,前边符号为加。
行列式按行按列展开法则。

行列随便换?加减乘除?
代数余子式,
前边是符号,
(-1)i+j次方 和为偶数为正 和为奇数为负
如果一行除了某一个数都为0 那么这个行列式 = aij 和它代数余子式的乘积。
行列式等于它的任一行,或者列的个元素与其代数余子式乘积之和。
任何行列式可以进行行的加减做法。 转换成三角行列式。
最终 的结果就是p11一直乘到pkk 主对角线,左上到右下。
不懂了后边。
行列式换列 变符号
将左下角,左半块变成0
换行,环列,一行整体加减另一行,只改变当前行列。
根据性质
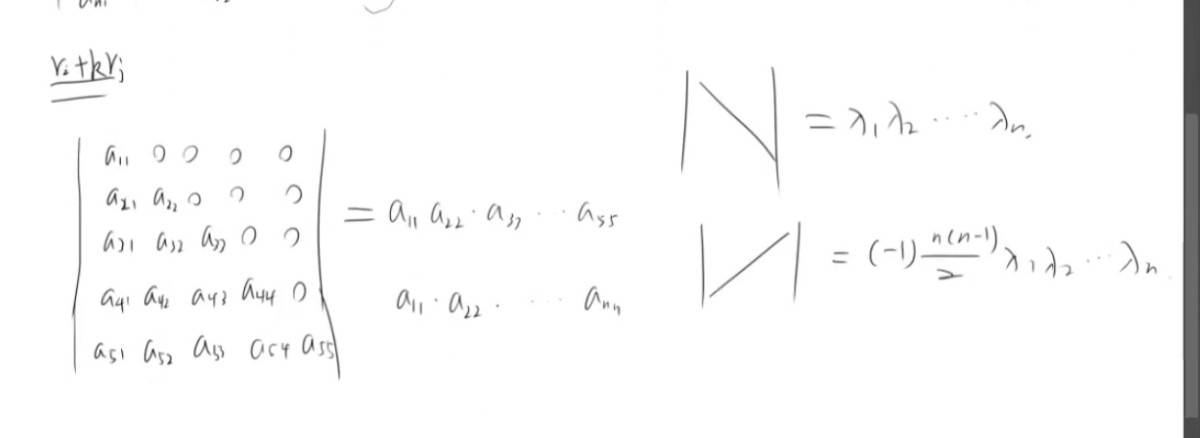
行列式,某行或某列可以拆 拆成两个行列式相加。
行列式与它的转置行列式相等
互换行列式,行列式变号
行列式某一行中所有元素都乘以同意数k,等于用数k乘以此行列式。
行列式中如果有两行成比例,那么此行列式为0
行列式某一行或者列的元素都是两数之和,那么这个可以拆成两个行列式相加。
把行列式某一行的元素乘以同一数然后加到零一行上,行列式不变。