矩阵乘法特点。
单位矩阵是从左到右斜线。
矩阵乘以单位矩阵还是自己。
转置就是行变列, 列变行
AB 不等于 BA 矩阵相乘
(AB)C = A(BC)分配律 就是先干谁都一样
(KA)B = K(AB) = A(KB) 满足交换律,
(AB)的转置 = B转置 *A 的转置
推导 。 右上角小t代表转置
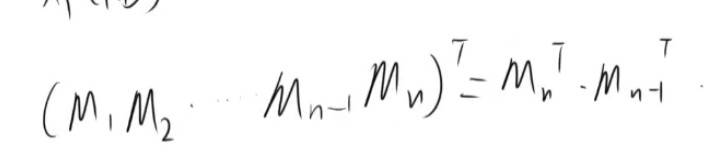
矩阵乘法特点。
单位矩阵是从左到右斜线。
矩阵乘以单位矩阵还是自己。
转置就是行变列, 列变行
AB 不等于 BA 矩阵相乘
(AB)C = A(BC)分配律 就是先干谁都一样
(KA)B = K(AB) = A(KB) 满足交换律,
(AB)的转置 = B转置 *A 的转置
推导 。 右上角小t代表转置
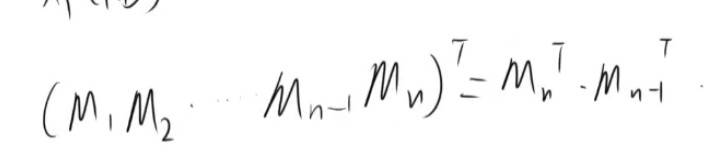
矩阵乘法
用行去乘列。 前一个矩阵的列数等于要乘的矩阵的行数。
矩阵的乘法 需满足条件
R*N N*C 前边的列数必须等于后边的行数才行。 乘完后是 R*C阶矩阵
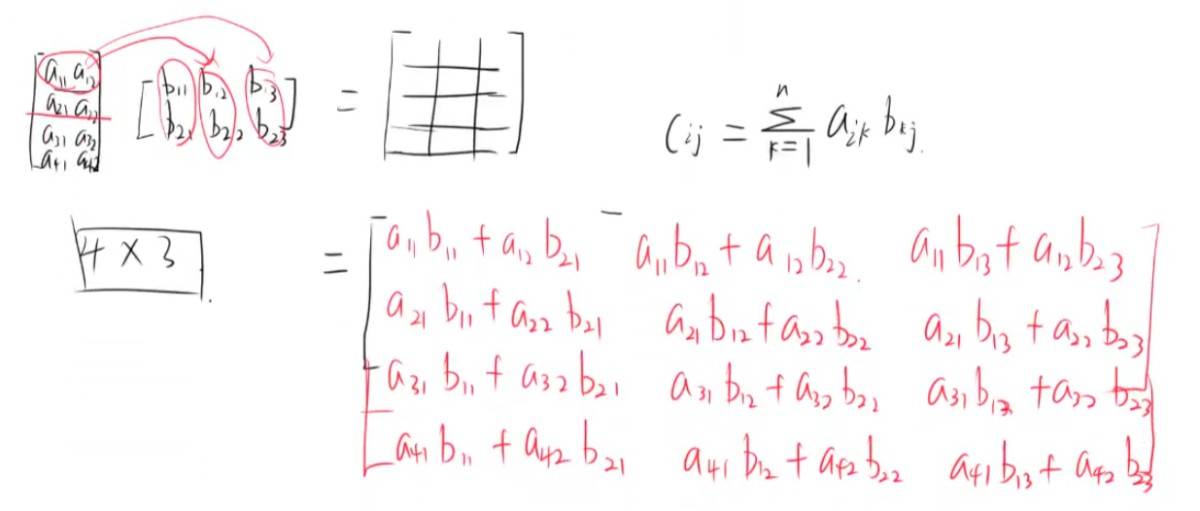
转置 行变列, 列变行 Mt
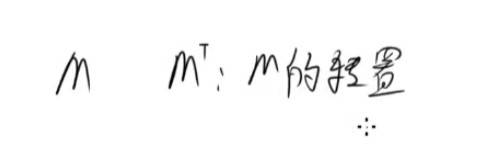
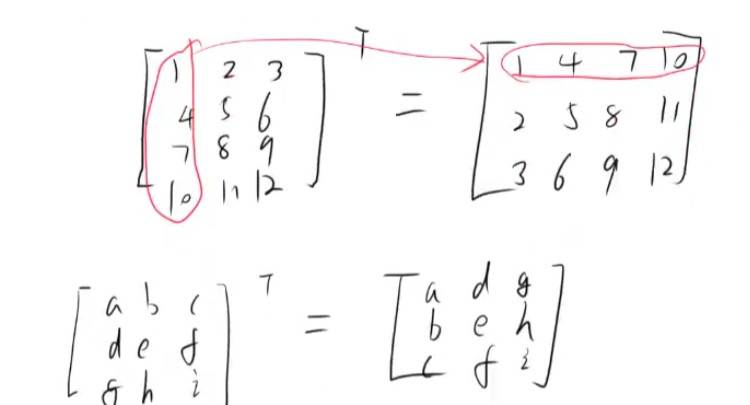
对角矩阵 专置 等于它本身。
标量与矩阵乘法。 直接乘到每个元素上。

转置就是行变列,列变行。
乘法类似,行*列,其间元素相加。
加法就是同行同列元素相加。
矩阵与向量。
矩阵和向量坐标
行向量 1*n矩阵
列向量 N*1矩阵
向量与矩阵运算时一定要确定 是行向量还是列向量
方阵 正方形阵 n*n
非对角线以外全是0的,并且是方阵的,叫对角矩阵
对角线全为1 非对角线全为零 叫单位矩阵 是对角矩阵的一部分。 单位矩阵在乘法中就是1 的作用。
矩阵 数字块
矩阵分行列
3*4阶矩阵
简单认识
矩阵是中括号。
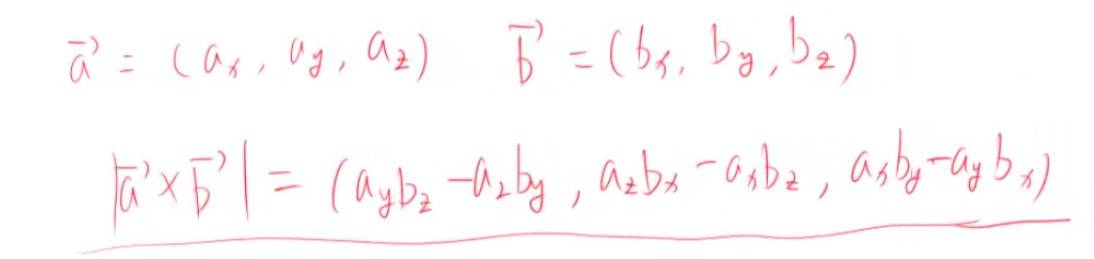
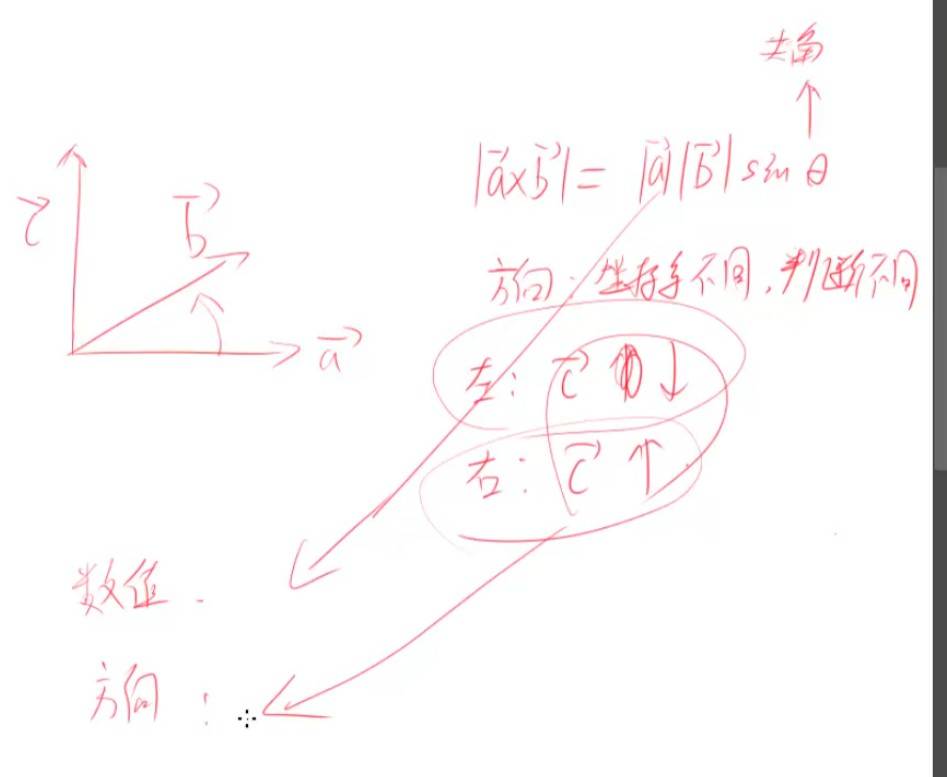
叉乘的意义 判断三角面片朝向
左手坐标系和右手坐标系不同。 产生方向不同,按右手坐标系来。
垂直向量生成
叉乘结果的模长等于两向量构成的平行四边形的面积,
取模长的一半即可
若两向量叉乘结果为零向量,则它们共线或反向
叉乘方向反映从第一个向量到第二个向量的旋转方向
法线是垂直,正交也是垂直
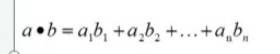
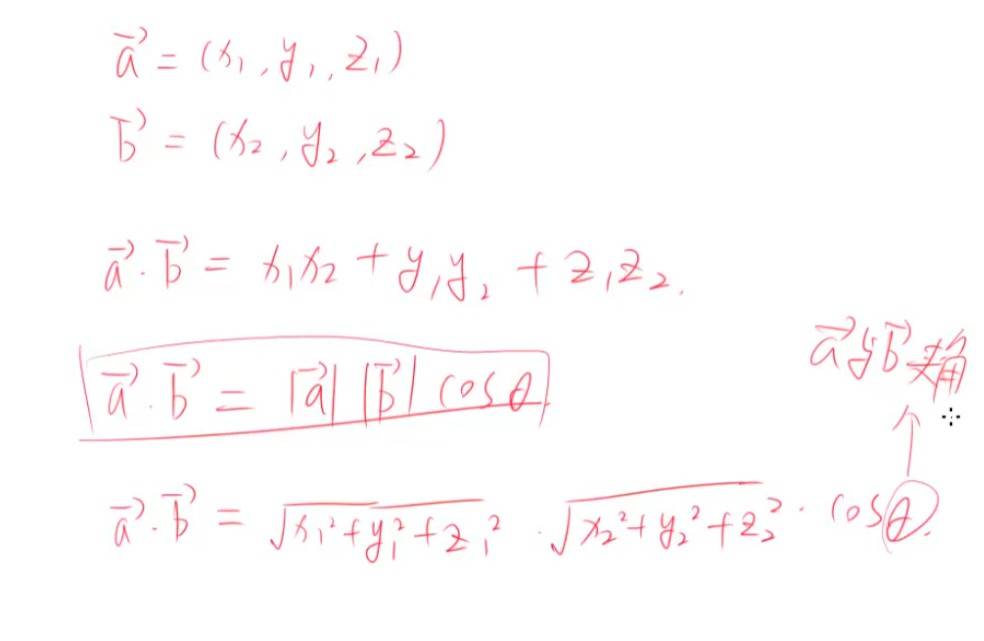
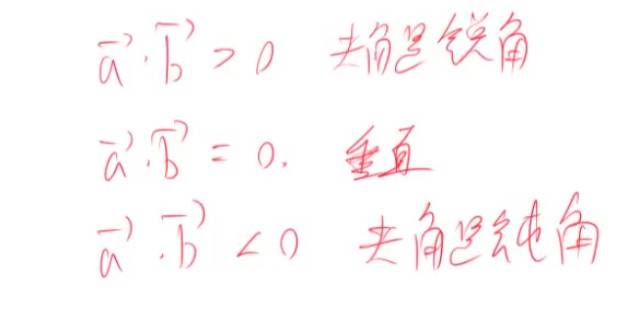
点积 也就是点乘 其实就是 向量之间的投影。
通过夹角判断两个物体的前后关系。
三位向量基础运算
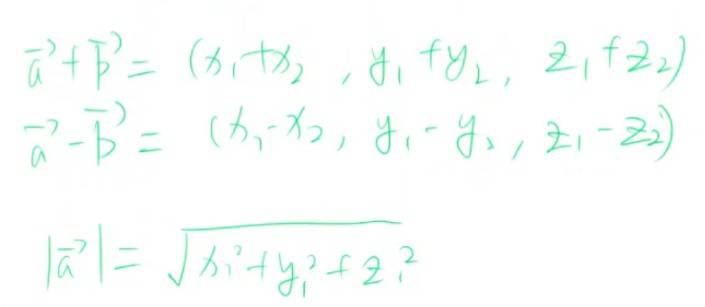
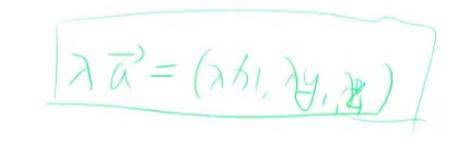
二维坐标系可以对称
三位的左右手坐标系 没办法转换
二维坐标系转换
x = x'cos日+y'sin日+a
y = y'cos日+x'sin日+b
向量计算必须在同一个坐标系下。
平移和旋转求新值。有公式。 公式再来找吧。
x' = x+a
y' = y+b
二维坐标系平移求新值。
不同坐标系转换
将坐标系旋转后
点坐标系旋转后,点坐标
x' = xcos日+ysin日
y' = ycos日 - xsin日
日为正,逆时针 日为负 顺时针
二维坐标系旋转求新值。
回顾总结。
单位向量。normalized
长度为1的向量。
零向量指代任意方向。
叉乘,向量积,外积,最后结果是 向量。
判断敌人在左前方还是右前方。
叉乘就是求出第三条垂直于当前两个向量平面的向量。
点乘求两个向量间的夹角
叉乘就是求垂直于两个向量的第三个向量。
点乘判断两个向量的关系 意义求夹角。
判断敌人在前在后。
两个向量点乘大于0 时,向量夹角为锐角。
两个向量点乘等于0时,向量夹角为直角。
两个向量小于0,向量为钝角。
向量点乘 点积
向量a*向量b = x1X2+Y1Y2 = 标量(数字)
几何意义
向量a乘以向量b = a的模乘以b的模乘以cos 日。
C方 = a方加b方减去2倍的a模乘以b模乘以cos日。
计算投影。 点乘。
a方加b方等于c方 勾股定理
根号8 = 2 倍根号2
向量的模 (长度) 根号下a方加b方
sin x = 对边比斜边。
sin 正弦 对边比斜边 cos 余弦 临边比斜边。
sin 30度 = 1/2
cos 30度 = 根号3/2
对边比斜边, 斜边是左侧的 ,临边是右侧的。
sin 对边比左边 cos 右边比左边。