A 的转置才为伴随矩阵    转置矩阵就是行变列，列变行

矩阵相乘   就是行*后边的一列  作为一个元素。

逆矩阵   *矩阵等于单位矩阵。

线性变换的可逆性，就是能放进去，也能放回来。用于还原。

伴随矩阵  

每个元素都是矩阵里每个元素的代数余子式  叫伴随矩阵。加转置。  

代数余子式，根据下标   结果有正负号。  奇数为负  偶数为正。  

行列随便换？加减乘除？

代数余子式，

前边是符号，

（-1）i+j次方   和为偶数为正   和为奇数为负

如果一行除了某一个数都为0  那么这个行列式 = aij 和它代数余子式的乘积。  

行列式等于它的任一行，或者列的个元素与其代数余子式乘积之和。  

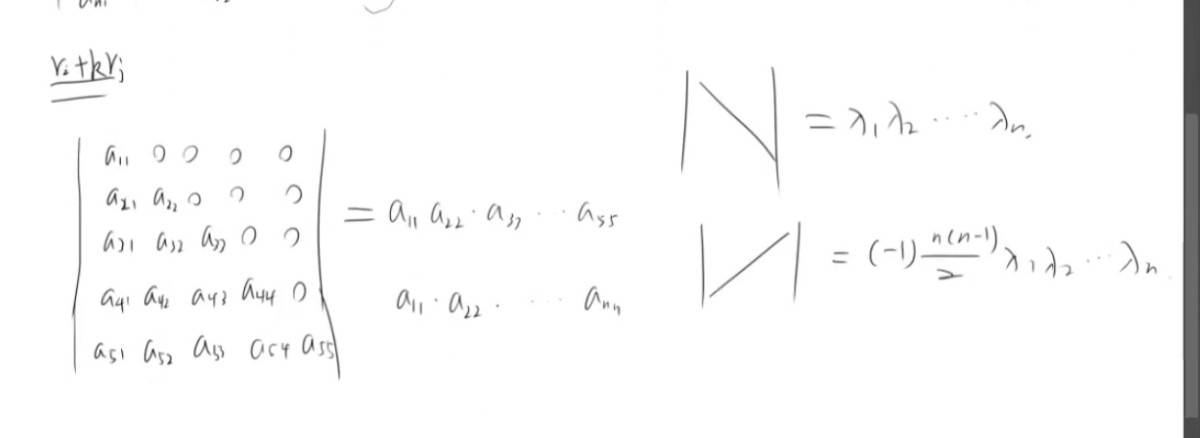
行列式，某行或某列可以拆   拆成两个行列式相加。

行列式与它的转置行列式相等 

互换行列式，行列式变号  

行列式某一行中所有元素都乘以同意数k，等于用数k乘以此行列式。

行列式中如果有两行成比例，那么此行列式为0

行列式某一行或者列的元素都是两数之和，那么这个可以拆成两个行列式相加。

把行列式某一行的元素乘以同一数然后加到零一行上，行列式不变。

二阶行列式

矩阵的行列式。 

每个矩阵都有对应的行列式，算出来是一个标量

|m|  这种写法

算法就是主对角线相乘减去副对角线   

左上到右下为主对角线

右上到左下为副对角线

行列式   符号和矩阵有所区别。  

有点牛逼，还能和初中的二元一次方程联动。

行列式的值。主对角线乘积的和减去相反斜对角线。

切变  不常用

长方形拉伸，面积不发生变化。属于图形变换的一种。

切变矩阵   

任意方向三维缩放矩阵。

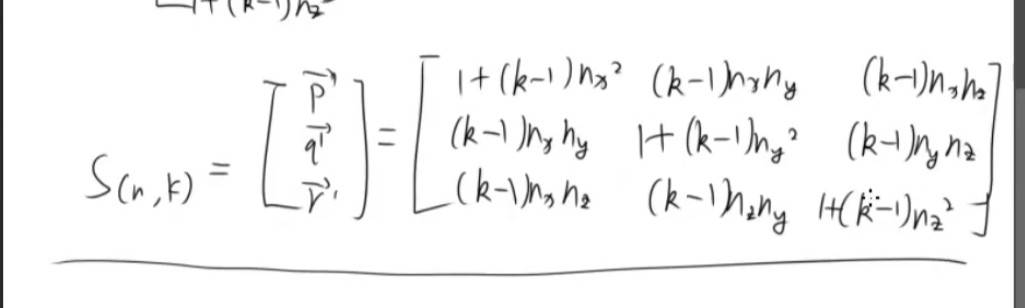
公式

控制图像进行变化，

正交投影包含向量点乘。  

向量向轴，平面，任意平面投影，正交就是垂直。就是把物体可以压缩成平面。

 叉乘公式，真叉乘，斜着乘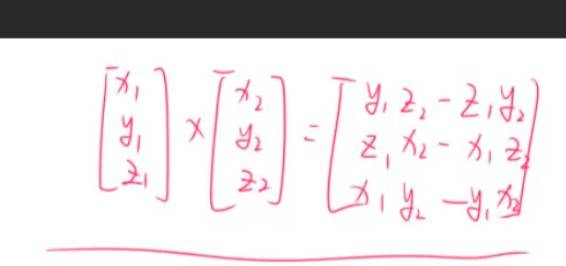

具体内容不太懂了

旋转矩阵就是为了改变向量，或者说图形位置。通过矩阵，将向量进行变化。最终达到改变图形位置的目的。

向量   矩阵  相乘  前边的列要等于后边的行数。才能相乘 

向量放矩阵左边叫左乘   

向量放矩阵右边叫右乘  

行向量左乘矩阵     列向量右乘矩阵   才有意义，不然不能算。 

DirectX  行向量   向量乘矩阵  在左在右，左乘右乘。两者结果不同。 

OpenGl 列向量  

转置     行变列，  列变行    Mt

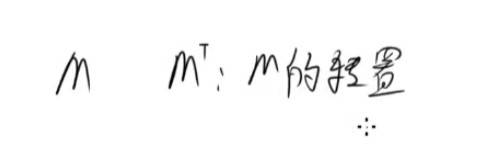
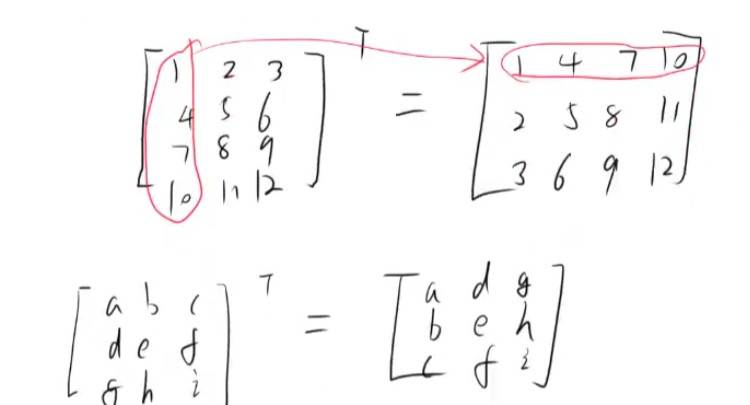
对角矩阵  专置 等于它本身。

标量与矩阵乘法。   直接乘到每个元素上。  

转置就是行变列，列变行。  

乘法类似，行*列，其间元素相加。 

加法就是同行同列元素相加。

矩阵  数字块

矩阵分行列

3*4阶矩阵

简单认识

矩阵是中括号。  

 二维坐标系转换

x = x'cos日+y'sin日+a

y = y'cos日+x'sin日+b

向量计算必须在同一个坐标系下。

平移和旋转求新值。有公式。  公式再来找吧。  

x' = x+a 

y' = y+b

二维坐标系平移求新值。

不同坐标系转换   

将坐标系旋转后  

点坐标系旋转后，点坐标

x' = xcos日+ysin日

y' = ycos日 - xsin日  

日为正，逆时针    日为负 顺时针

二维坐标系旋转求新值。

单位向量。normalized   

长度为1的向量。 

零向量指代任意方向。  

叉乘，向量积，外积，最后结果是  向量。

判断敌人在左前方还是右前方。

叉乘就是求出第三条垂直于当前两个向量平面的向量。

点乘求两个向量间的夹角  

叉乘就是求垂直于两个向量的第三个向量。

向量点乘  点积  

向量a*向量b = x1X2+Y1Y2 = 标量(数字)

几何意义 

向量a乘以向量b = a的模乘以b的模乘以cos 日。 

C方 = a方加b方减去2倍的a模乘以b模乘以cos日。

计算投影。   点乘。 

a方加b方等于c方   勾股定理  

根号8  =   2 倍根号2  

向量的模   （长度）   根号下a方加b方

sin x  = 对边比斜边。 

sin 正弦  对边比斜边  cos 余弦  临边比斜边。

sin 30度 = 1/2

cos 30度 = 根号3/2

对边比斜边，   斜边是左侧的   ，临边是右侧的。 

sin 对边比左边    cos 右边比左边。   

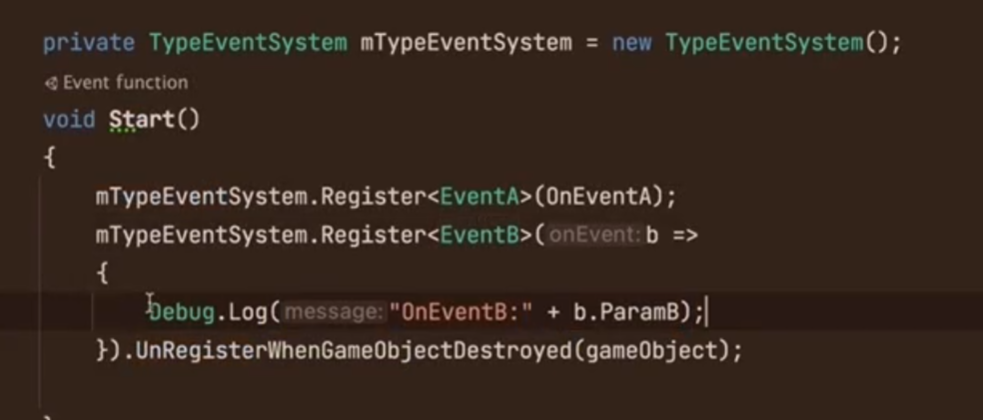
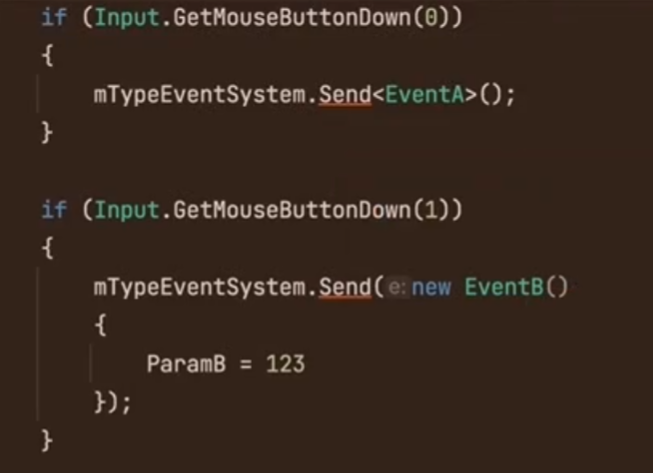
事件是从底层系统层向表现层发送的

UnRegisterOnDestoryTrigger挂到一个对象上，对象销毁的同时，时间也会相应注销

向量相减就是  x减x y减y  

平行四边形的对角，   

向量的加减属于这个。