三角形法则。
向量相加就是,x加x y加y
AB+BC = AC 首尾相连
向量平移
三角形法则。
向量相加就是,x加x y加y
AB+BC = AC 首尾相连
向量平移
高维行列式转低维 通过按行按列展开。
行列式的结果等于一行的单个数乘以他们的 代数余子式 下标为奇数,前边符号为减 下表为偶数,前边符号为加。
行列式按行按列展开法则。

任何行列式可以进行行的加减做法。 转换成三角行列式。
最终 的结果就是p11一直乘到pkk 主对角线,左上到右下。
不懂了后边。
行列式换列 变符号
将左下角,左半块变成0
换行,环列,一行整体加减另一行,只改变当前行列。
根据性质
流程总结,可以直接看这。
顶点着色器 顶点是独立的 位置变化,光照
顶点动画 波浪之类的
裁剪就是在视野范围内的保留,一半在内一半在外的同理,只保留视野内的
矩阵的余子式
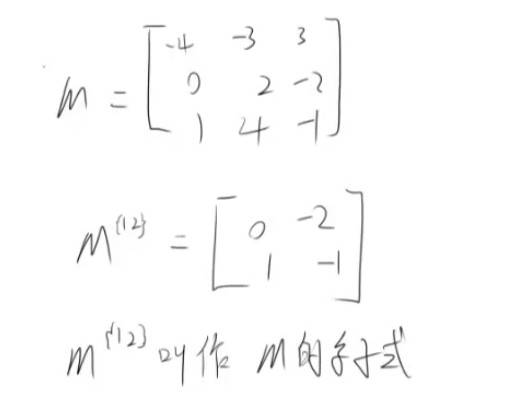
去掉某行某列,剩余的叫余子式。
矩阵的 代数余子式 求标量值
行列式有一些性质。

三阶行列式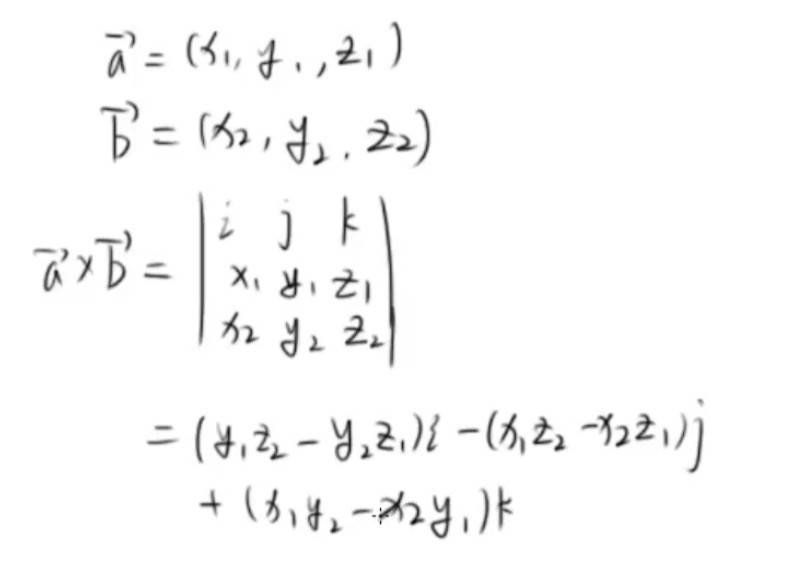
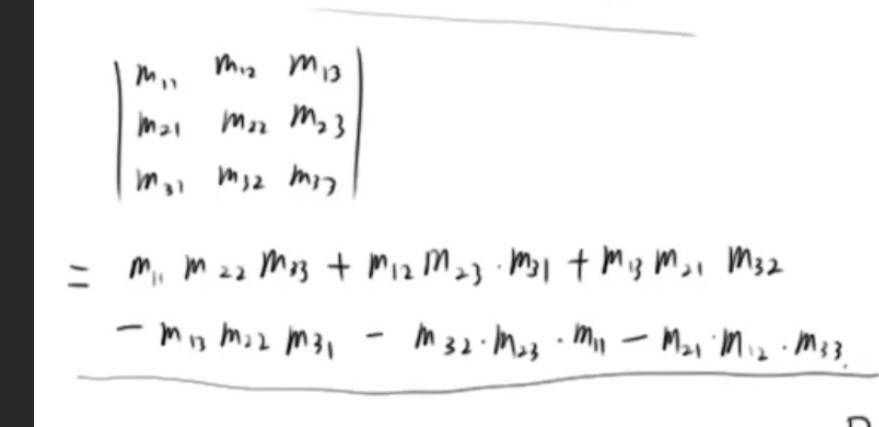
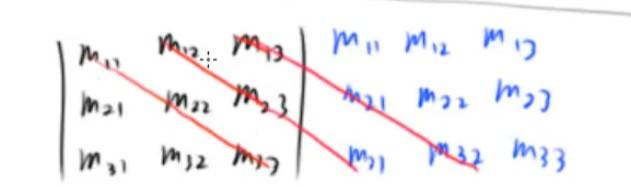
不太好描述, 左上到右下,凑够三条线 减去
右上到左下 凑够三条线 (每条线3个数)
本质还是对角线。
叉乘相当于求行列式。
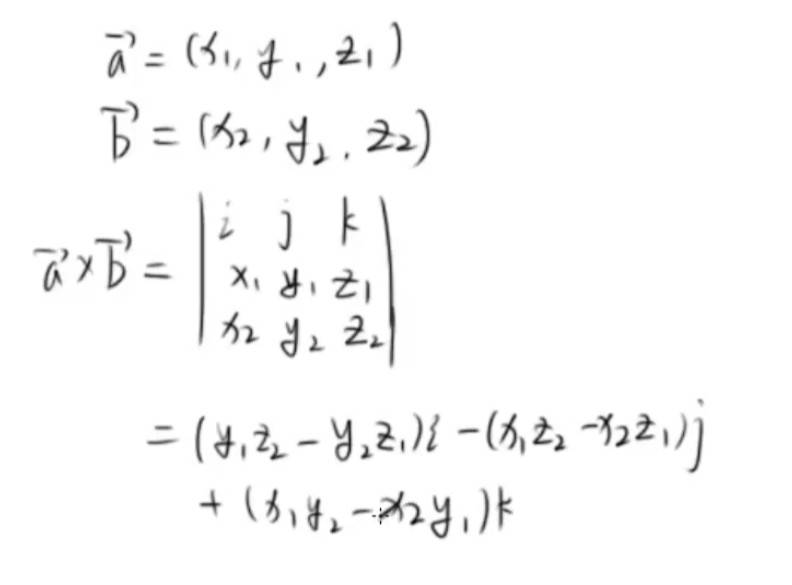
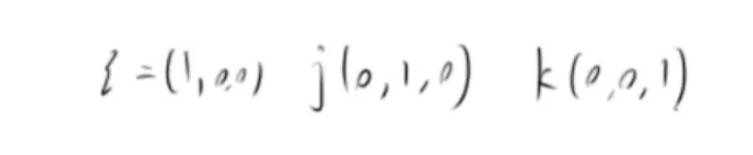
最后结果。
变换的组合
不是很懂,
物体坐标,到世界坐标,再到屏幕坐标(相机坐标)
物体坐标到相机坐标。
镜像矩阵
缩放因子为0 代表投影
缩放因子为-1 代表镜像。
P(n) = S(n向量,0) P(n) = S(n向量,-1)
矩阵和向量图形有关了,投影镜像这些。
二维的。
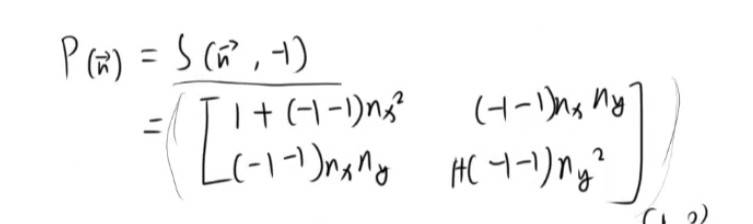
公式。
三维
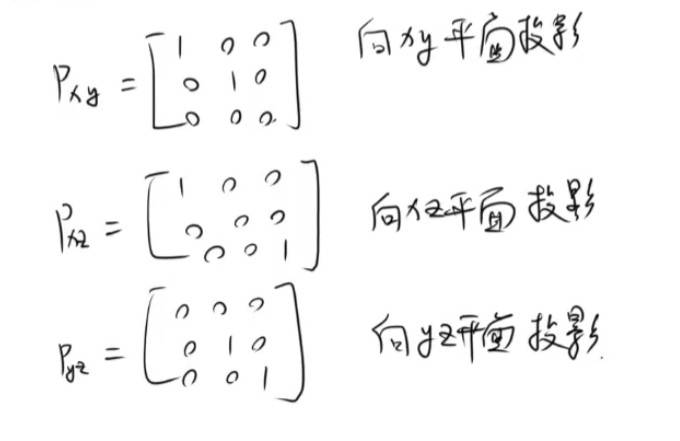
正交投影矩阵
向任意直线投影的矩阵公式
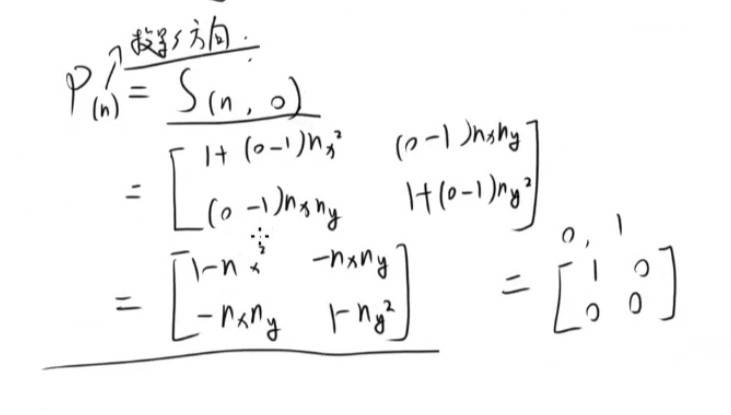
不懂,直接整最后结果 。
向任意平面投影的矩阵公式
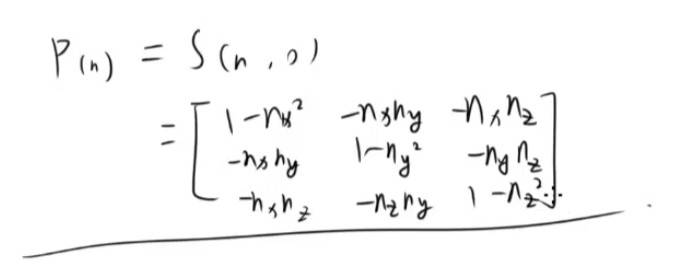
正交投影 降维 三维变二维 二维变一维 投影。
矩阵描述
通过数学进行图像表达。
缩放二维矩阵
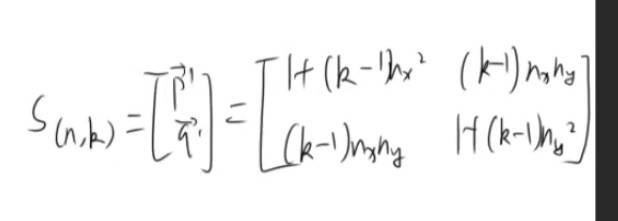
公式
好的,还是听不懂
均匀缩放 等比例缩放
非均匀缩放
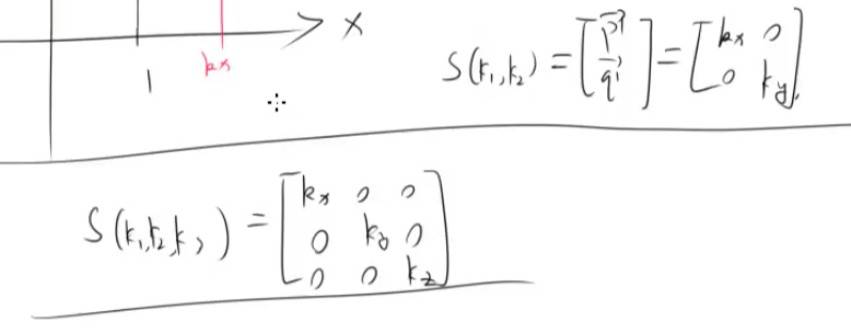 沿轴缩放得到对角矩阵。
沿轴缩放得到对角矩阵。
三位绕任意轴旋转。
三维绕轴旋转矩阵
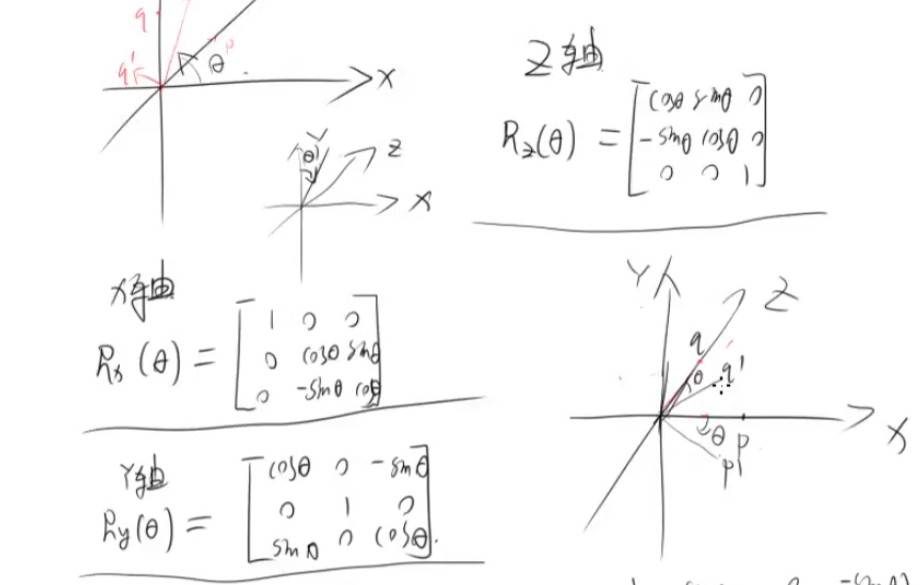
听不是太懂了。
旋转
基向量就是(0,1) (1,0)这些
变换物体与变换坐标系。
物体旋转和坐标系旋转,位置都会变化
旋转坐标系相当于以相反的量旋转物体。